Matryoshka Sparse Autoencoders
Search through latents with a token-regex language
View trees here
View individual latents here
See code here (github.com/noanabeshima/matryoshka-saes)
Abstract
Sparse autoencoders (SAEs) break down neural network internals into components called latents. SAE latents seem to correspond to more abstract concepts while larger SAE latents seem to represent finer, more specific concepts.
While increasing SAE size allows for finer-grained representations, it also introduces two key problems: feature absorption introduced in Chanin et al. , where latents develop unintuitive "holes" as other latents in the SAE take over specific cases, and what I term fragmentation, where meaningful abstract concepts in the small SAE (e.g. 'female names' or 'words in quotes') shatter (via feature splitting) into many specific latents, hiding real structure in the model.
This paper introduces Matryoshka SAEs, a training approach that addresses these challenges. Inspired by prior work, Matryoshka SAEs are trained with a sum of SAE losses computed on random prefixes of the SAE latents. I demonstrate that Matryoshka SAEs completely avoid issues in a toy model designed to exhibit feature absorption in traditional SAEs. I then apply the method to a 4-layer TinyStories language model. My results demonstrate that Matryoshka SAEs reduce feature absorption while preserving abstract features.
Introduction
Sparse autoencoders (SAEs) help us break down neural network internals into more easily analyzeable pieces called latents. These latents may correspond to actual "features" the model uses for processing .
SAE size affects the granularity of learned concepts: smaller SAEs learn abstract latents, while larger ones capture fine details.
While some splitting of concepts is expected as we increase SAE size, my investigation reveals a consistent pattern of failure:
- At a certain size, an SAE latent represents an abstract concept (like "words in quotes" or "female names").
- In larger SAEs, this abstract concept develops holes—unexpected exceptions where other latents take over. This feature absorption seems to occur when one feature is highly linearly predictable from another and is likely an artifact of sparsity regularization.
- At sufficient size, the abstract feature disappears entirely, fragmenting into many specific latents (feature fragmentation).
These issues complicate interpretability work. Feature absorption forces accurate latent descriptions to have lists of special-cased exceptions. Feature fragmentation hides higher-level concepts I think the model likely uses.
Large SAEs offer clear benefits over small ones: better reconstruction error and representation of fine-grained features. Ideally, we'd have a single large SAE that maintain these benefits while preserving the abstract concepts found in smaller SAEs, all without unnatural holes.
While we could use a family of varying size SAEs per language model location, a single SAE per location would be much better for finding feature circuits using e.g. Marks et al's circuit finding method.
To address these limitations, I introduce Matryoshka SAEs, an alternative training approach inspired by prior work. In a toy model designed to exhibit feature absorption (similar to the model introduced in Chanin et al.), Matryoshka SAEs completely avoid the feature-absorption holes that appear in vanilla SAEs.
When trained on language models (the output of MLPs, attention blocks, and the residual stream), Large Matryoshka SAEs seem to preserve the abstract features found in small vanilla SAEs better than large vanilla SAEs and appear to have fewer feature-absorption holes.
Problem
Terminology
This makes them more comparable to sqrt or tanh sparsity functions. Details can be found here.
Reference SAEs
To study how SAE latents change with scale, I train a family of small vanilla "reference" SAEs of varying sizes (30, 100, 300, 1000, 3k, 10k) on three locations in a 4-layer TinyStories model (https://github.com/noanabeshima/tinymodel): attention block outputs, mlp block outputs, and the residual stream before each attention block. I refer to the 30-latent SAE as S/0, the 100-latent SAE as S/1, etc. where S/x denotes the x-th size in this sequence.
These reference SAEs can help demonstrate both feature absorption and how Matryoshka SAEs preserve abstract latents.
Throughout this paper, any reference SAE without a specified location is trained on the pre-attention residual stream of layer 3 (the model's final layer).
Feature Absorption Example
Let's examine a concrete case of feature absorption by looking at a female-words latent in the 300-latent reference SAE (S/2) and some handpicked latents it co-fires with in the 1000-latent SAE (S/3). S/2/65 (latent 65 of S/2) and S/3/66 look very similar to each other. If you're curious, you might try to spot their differences using this interface:
The root node, S/2/65, seems to fire on female names, ' she', ' her', and ' girl'. Some rarer tokens I notice while sampling include daughter, lady, aunt, queen, pink, and doll.
If you click on the right node, S/3/861, you'll see that it seems to be a Sue feature. S/3/359 is similar to the Sue latent but for Lily, Lilly, Lila, and Luna.
S/3/66, however, is very interesting. It's very similar , S/2/101, except for specific *holes—*it often skips Lily or Sue tokens! You can see this by clicking on S/2/65 and then hovering on-and-off S/3/66.
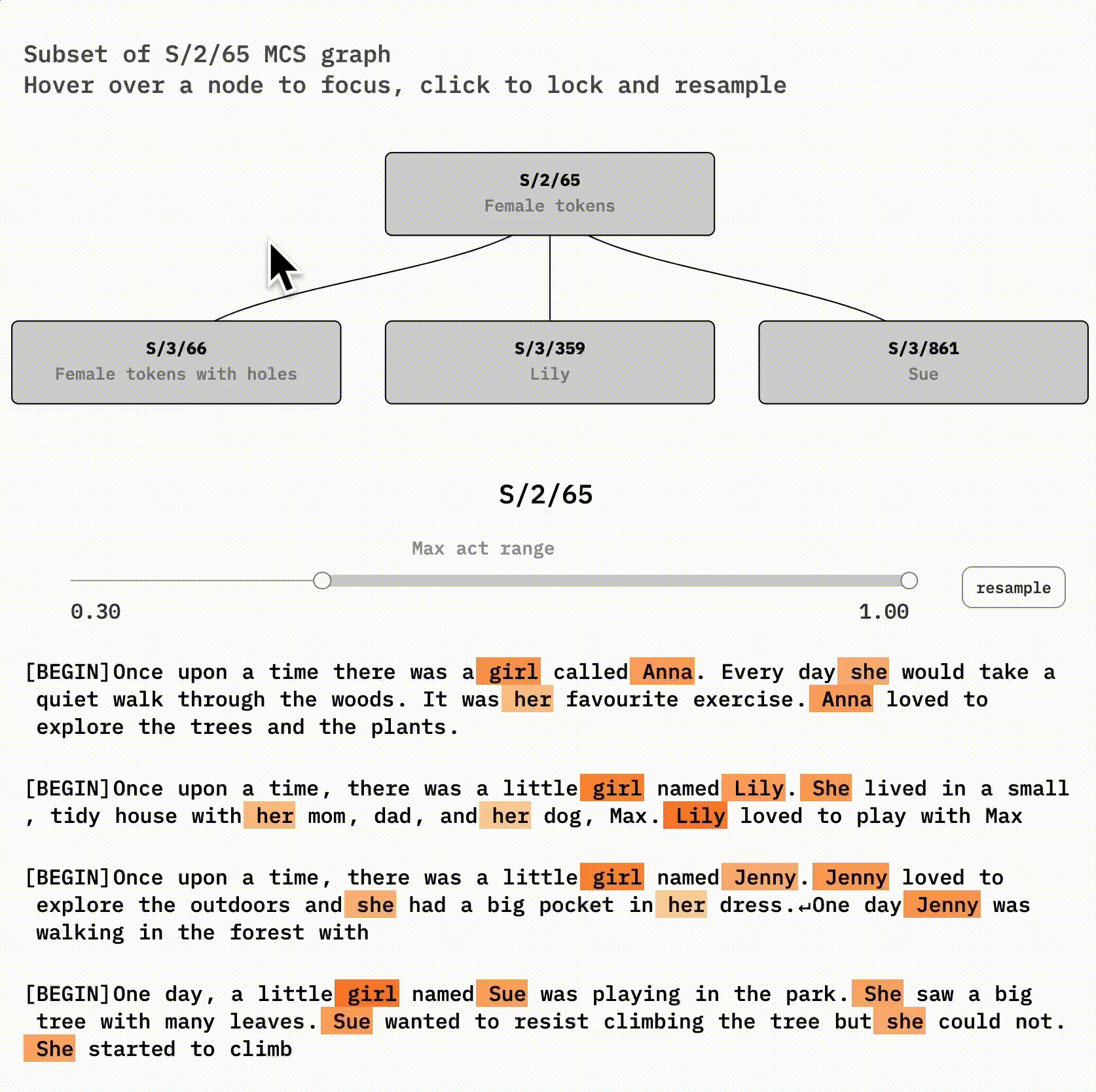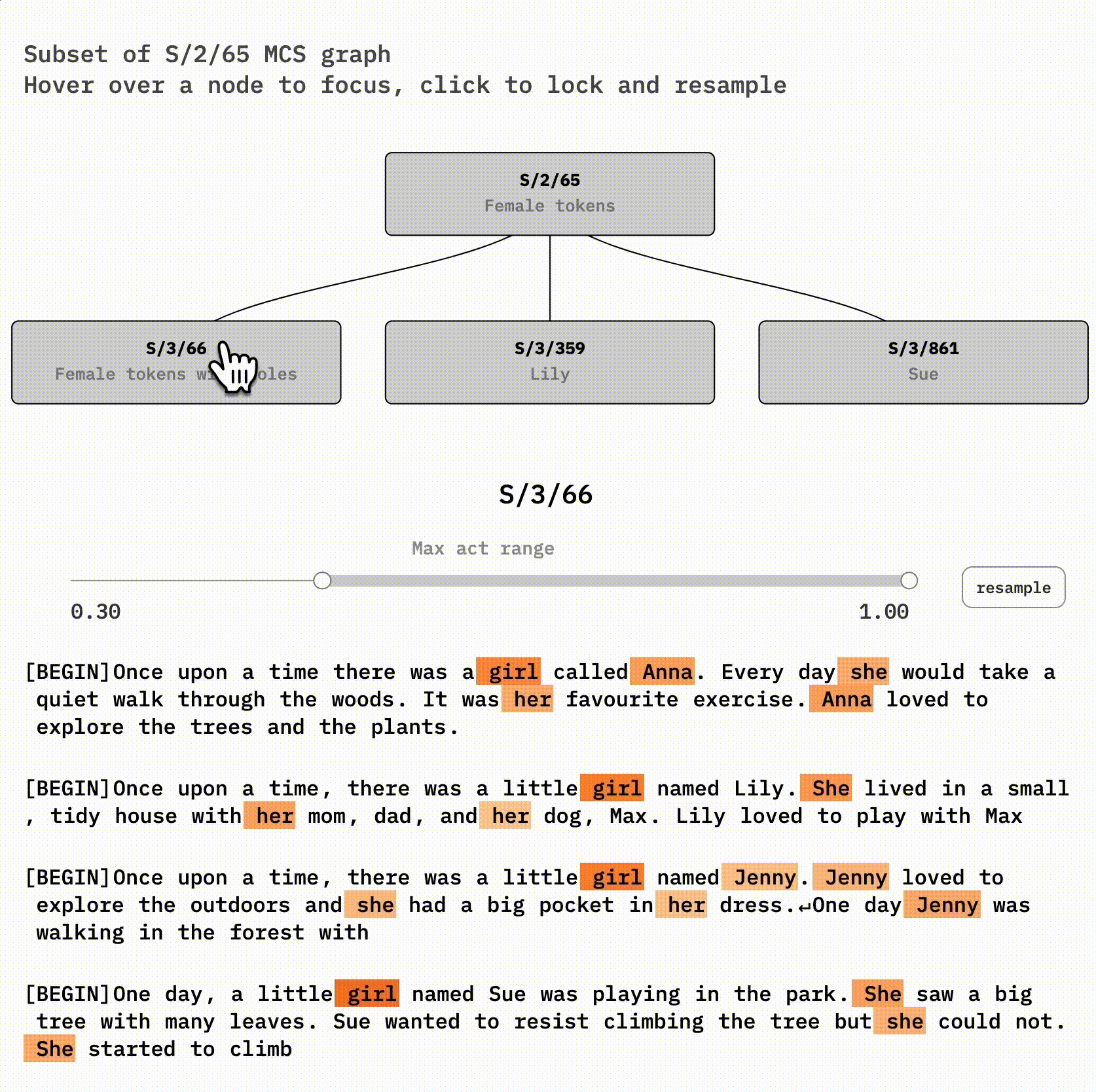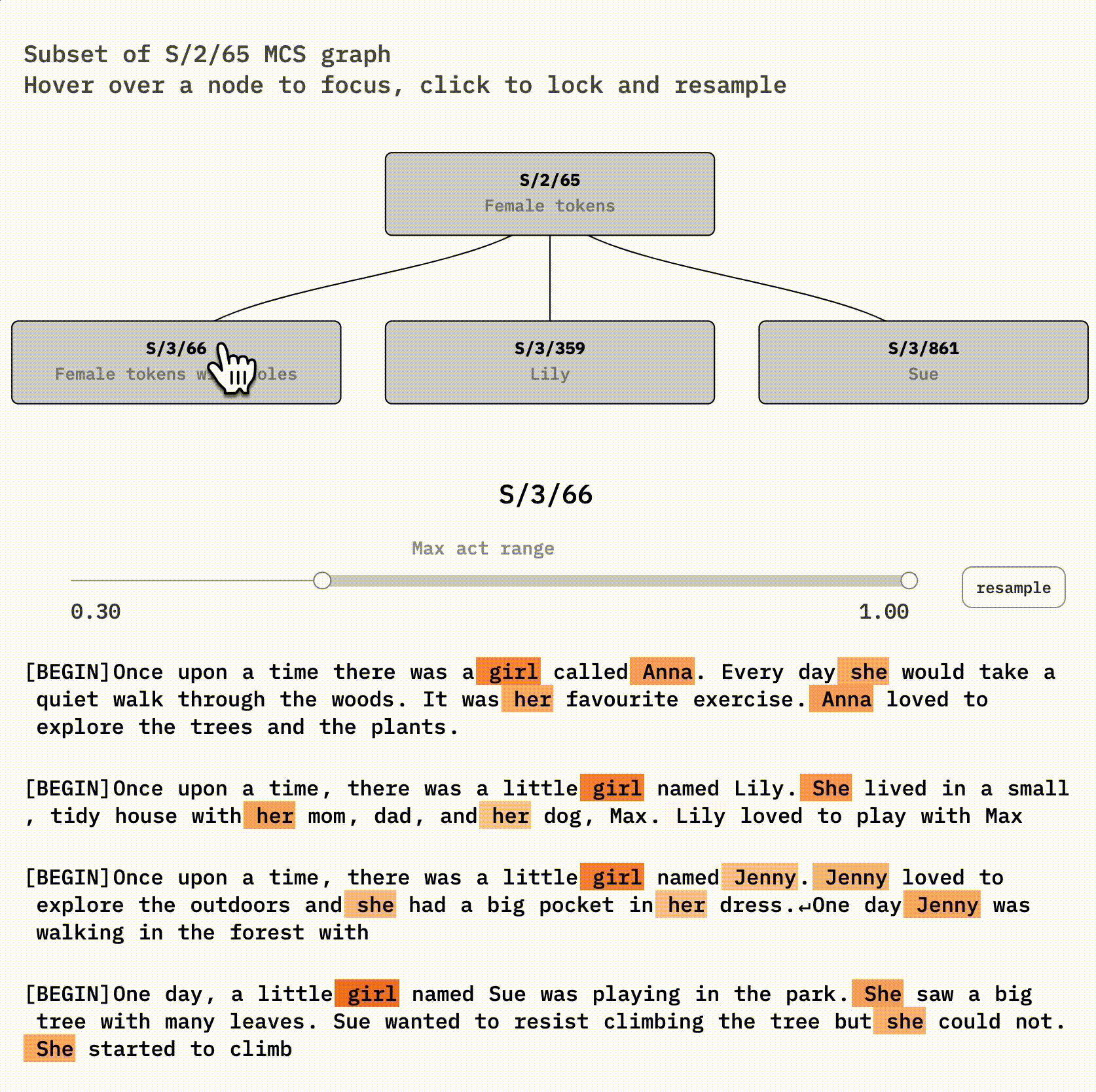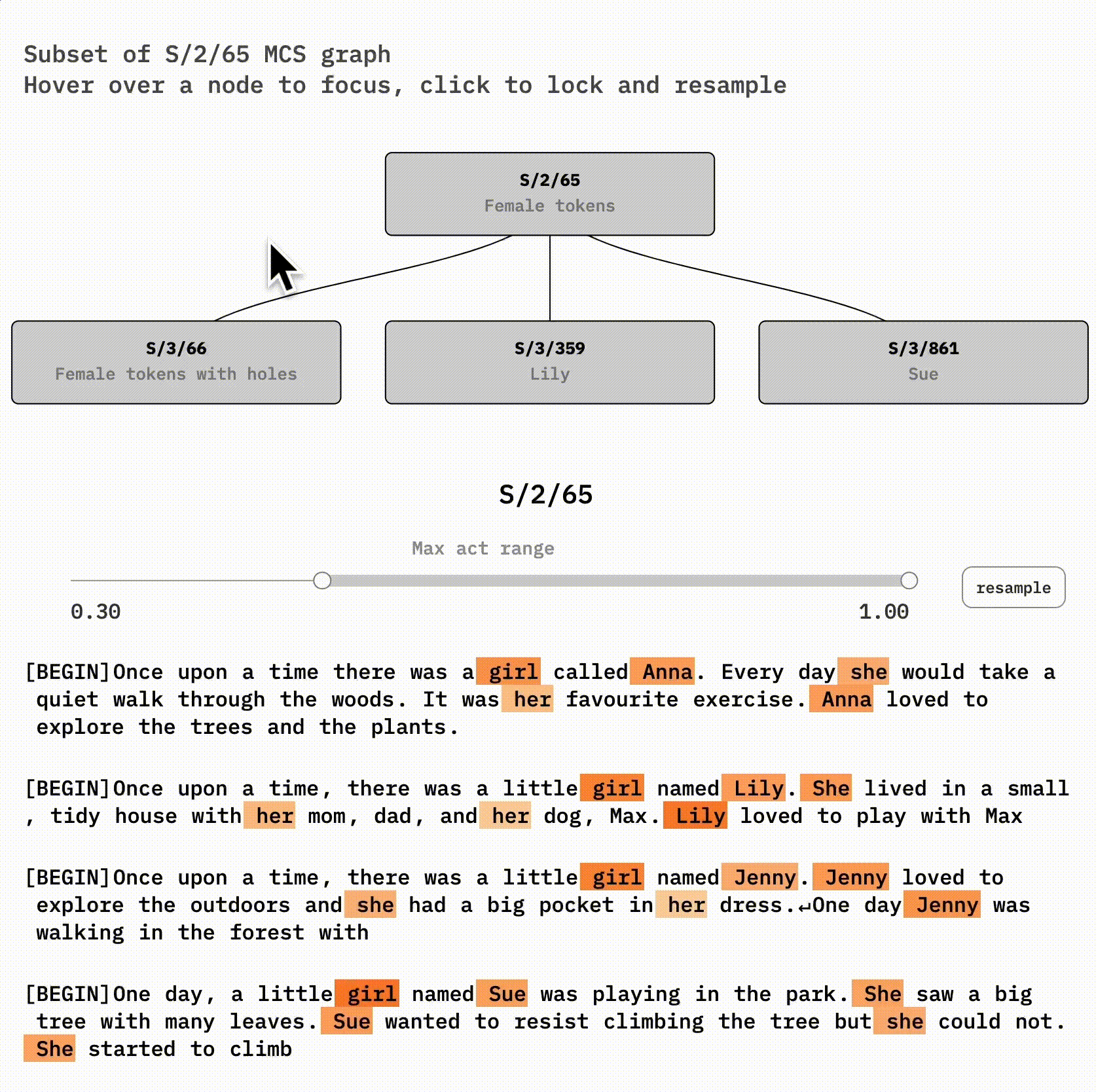
The abstract female concept is likely still implicitly represented in the SAE for Lily and Sue—it's included in the Lily and Sue latent decoder vectors. But we can't detect that just by looking at activations anymore. The concept has become invisible. In exchange, our larger SAE now represents the new information that Lily and Sue are distinct names.
Larger width SAEs with the same L0 stop representing a feature that fires on most female names. The feature has become fragmented across many latents for particular names. .
Feature fragmentation also complicates circuit analysis using SAEs (see Marks et al.). If a circuit uses a concept like 'this token is a name', we don't want to trace through 100 different name-specific latents when a single 'name' latent would suffice. On the other hand, if a circuit uses fine-grained features, we want our SAE to capture those too. When looking for a circuit, it is not obvious how to choose the appropriate vanilla SAE size for many different locations in the model simultaneously. And if the circuit depends on both an abstract and fine-grained feature in one location, no single vanilla SAE size is sufficient and it is unclear how to effectively integrate multiple sizes.
More examples of absorption and fragmentation can be found in https://sparselatents.com/tree_view.
Method
Consider how feature absorption might occur during SAE training:
- An abstract feature like "female tokens" and a specific case like "Lily" begin to be learned by different latents.
- Since "Lily" tokens always involve the "female tokens" feature, the sparsity loss pushes for encoding the "female" aspect directly in the "Lily" decoder vector.
- The "female tokens" latent stops firing on "Lily" tokens.
How can we stop the SAE from absorbing features like this?
What if we could stop absorption by sometimes training our abstract latents without the specific latents present? Then a "female tokens" latent would need to learn to fire on all female tokens, including "Lily", since there wouldn't be a consistent "Lily" latent to rely on.
This is the idea for the Matryoshka SAE: train on a mixture of losses, each computed on a different prefix of the SAE latents.

The Matryoshka SAE computes multiple SAE losses in each training step, each using a different-length prefix of the autoencoder latents. When computing losses with shorter prefixes, early latents must reconstruct the input without help from later latents. This reduces feature absorption - an early "female words" latent can't rely on a later "Lily-specific" latent to handle Lily tokens, since that later latent isn't always available. Later latents are then free to specialize without creating holes in earlier, more abstract features.
For each batch, I compute losses using 10 different prefixes. One prefix is the entire SAE, and the remaining prefix lengths are sampled from a truncated Pareto distribution. Always including the entire SAE prefix avoids the issue where SAE latents later in the ordering aren't trained on many examples because their probability of being sampled in at least one prefix is low.
their contribution to reconstruction—latents with larger squared activations (weighted by decoder norm) are moved earlier. This ensures that important features consistently appear in shorter prefixes.
A naive implementation would require 10 forward passes per batch, and could be quite slow. By reusing work between prefixes, my algorithm trains in only 1.5x the time of a standard SAE. Mathematical details and efficient training algorithm can be found in https://www.sparselatents.com/matryoshka_loss.pdf. Code can be found at github.com/noanabeshima/matryoshka-saes.
Results
Toy Model
To demonstrate how Matryoshka SAEs prevent feature absorption, I first test them on a toy model, similar to the model introduced in Chanin et al. , where we can directly observe feature absorption happening for vanilla SAEs.
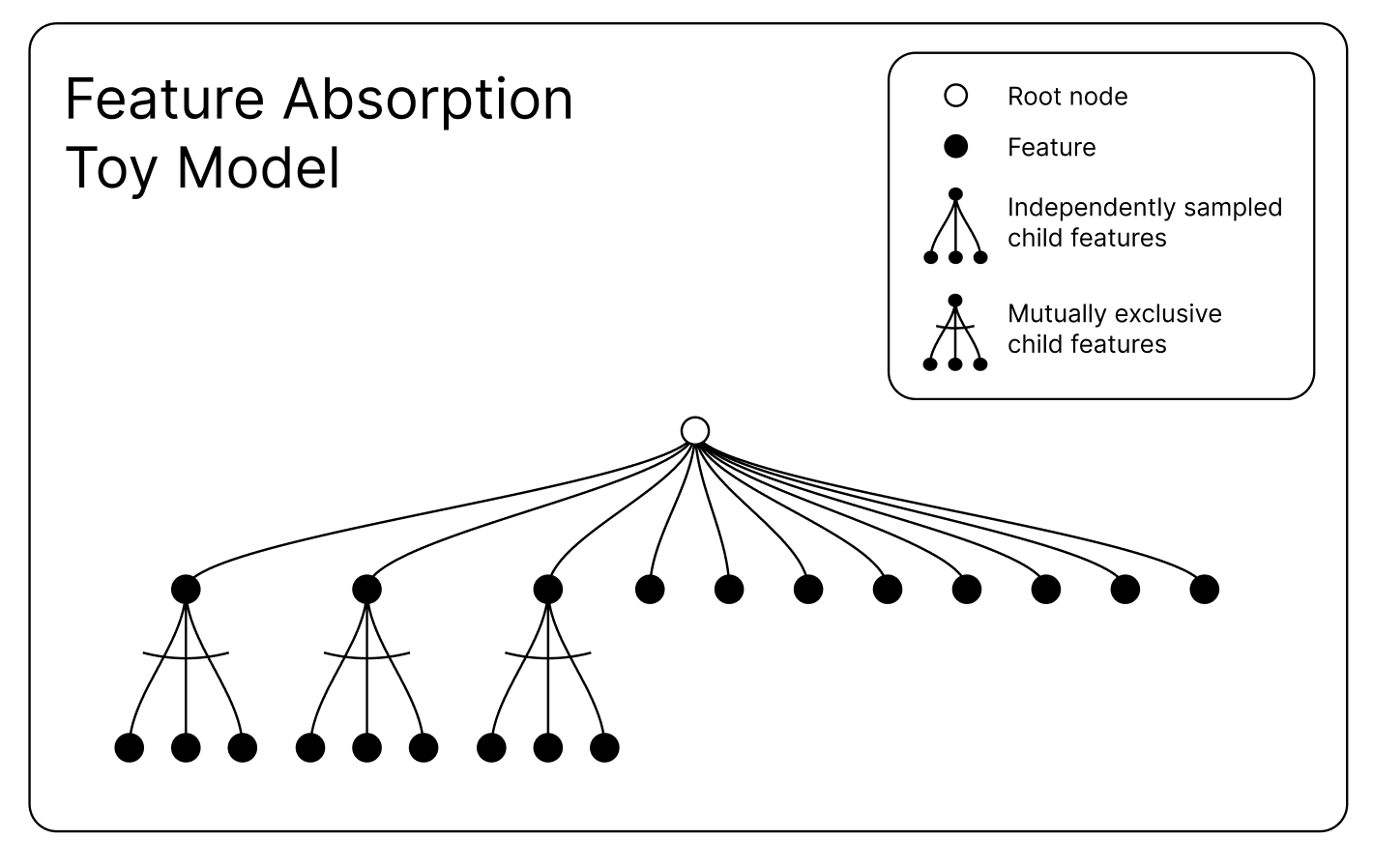
Features in this toy model form a tree, where child features only appear if their parent features are present. Just as "Lily" always implies "female name" in our language model example, child features here are always accompanied by their parent features.
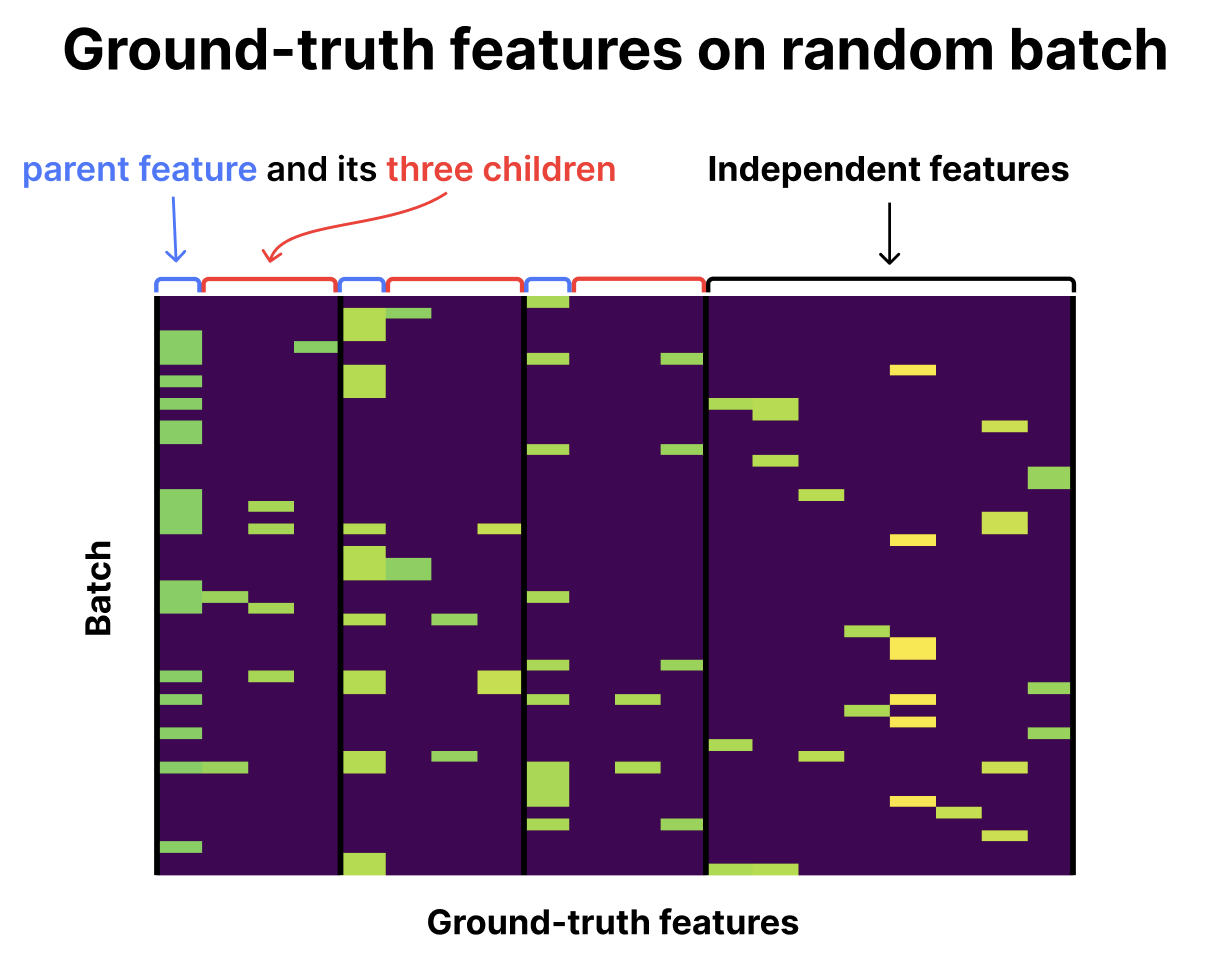
Each edge in the tree has an assigned probability, determining whether a child feature appears when its parent is present. . I set the number of SAE latents to the number of features.
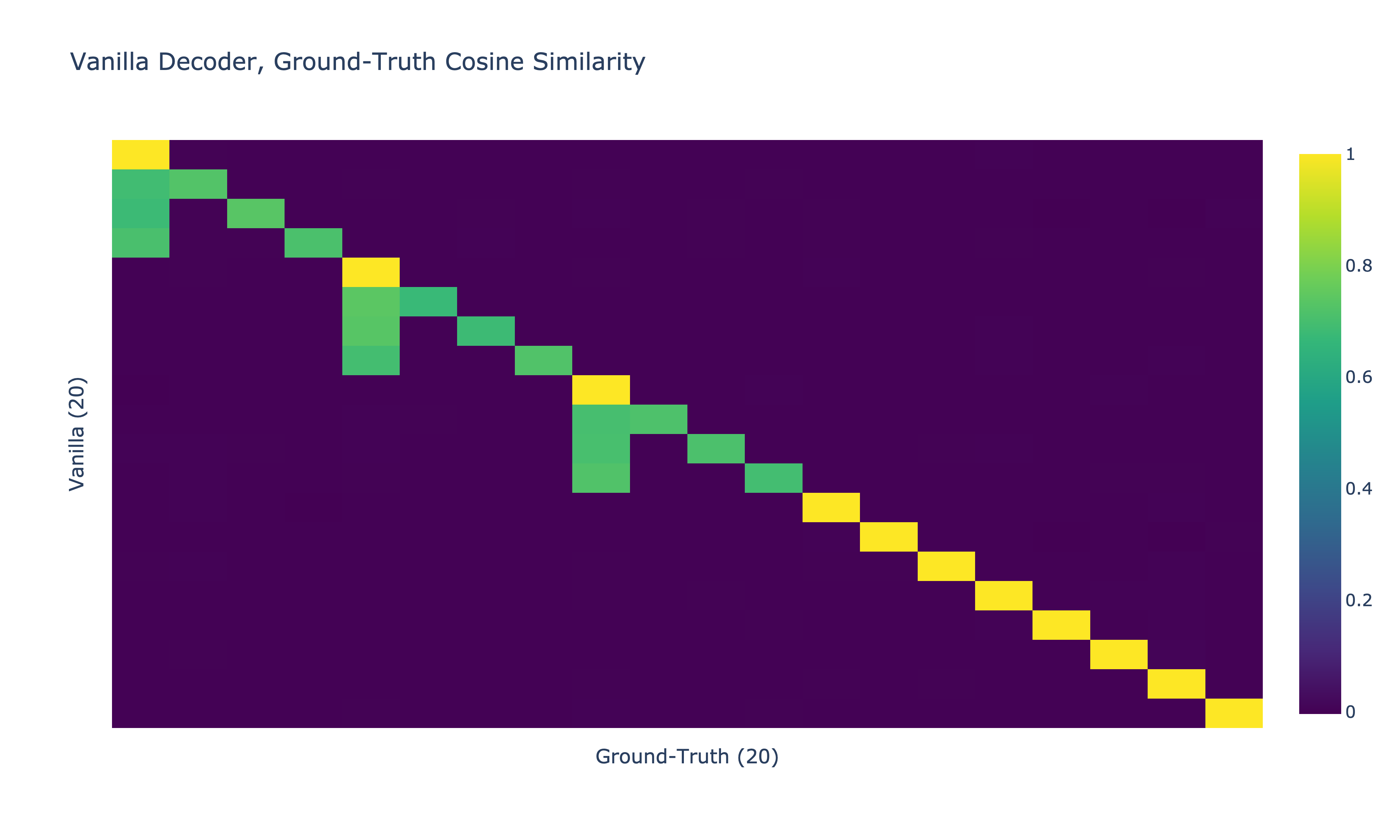
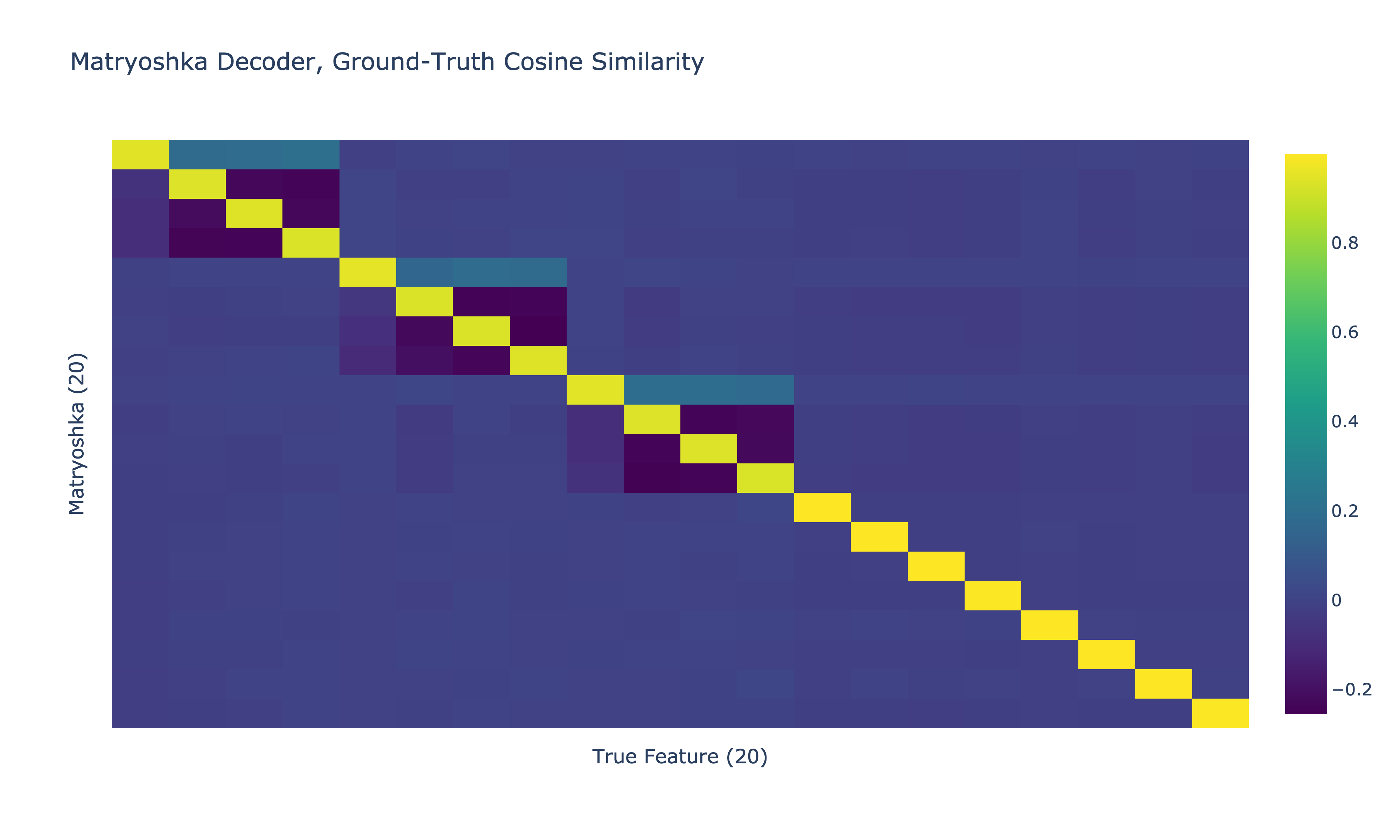
Let's look at how vanilla and Matryoshka SAEs learn these features after training for 20K steps with Adam. Below are the ground-truth features on a batch of data with all-zero entries filtered out.
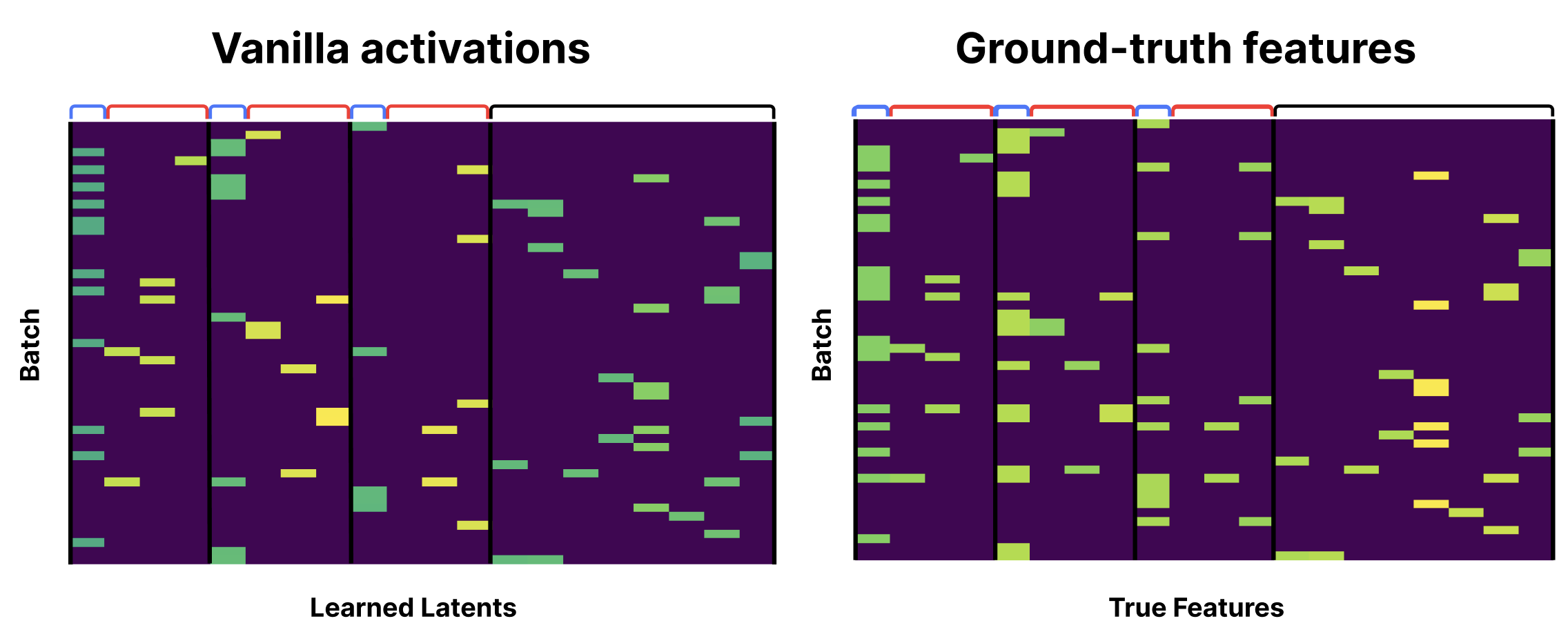
The vanilla SAE activations show feature-absorption holes—parent features don't fire when thei
The Matryoshka SAE latents, however, match the ground truth pattern—each latent fires whenever its corresponding feature is present.
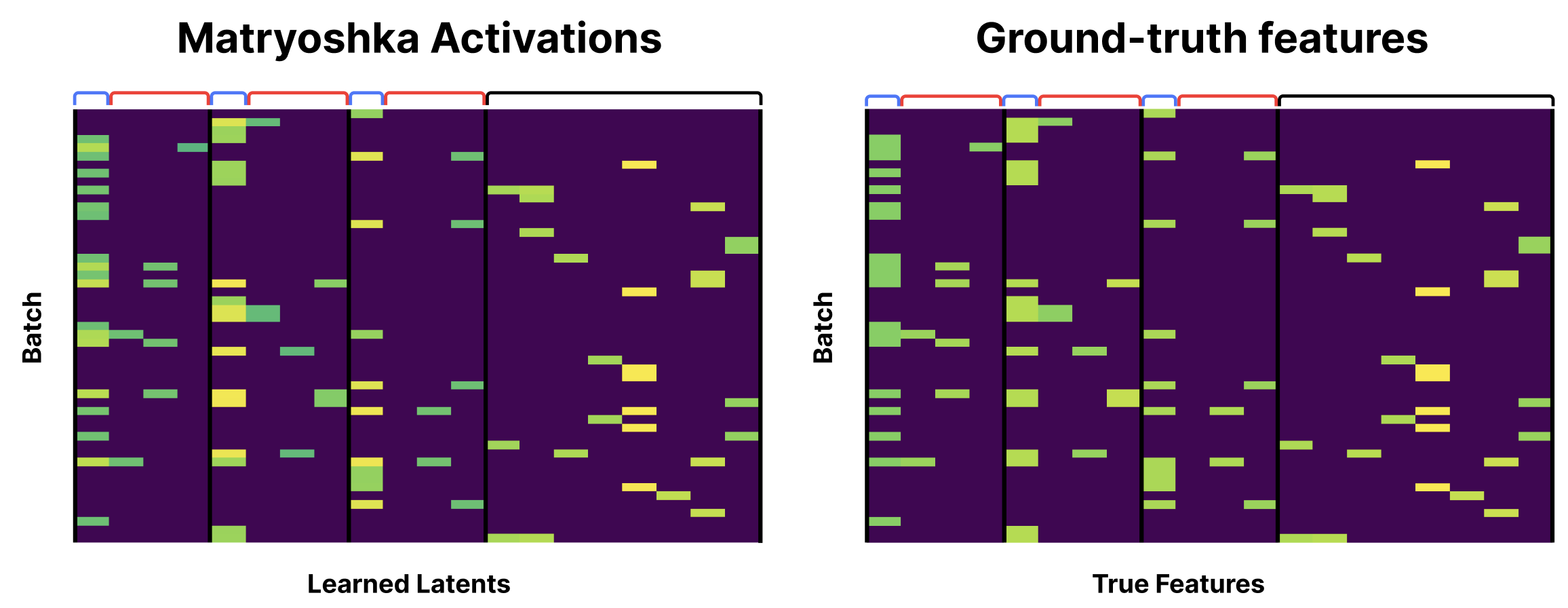
Interestingly, matryoshka parents tend to have slightly larger activations when their children are present.
Here are the cosine similarities between the ground truth features and the vanilla and Matryoshka SAE decoders.
Language Model Results
To test Matryoshka SAEs on real neural networks, I train and Matryoshka SAEs with varying L0s [15, 30, 60] on (the output of MLPs, attention blocks, and the residual stream) in a TinyStories language model. They're trained on 100M tokens, 1/3 the size of the TinyStories dataset.
Let's return to our female words example. Below, each reference SAE latent is shown alongside its closest match (by activation correlation) from both the 25k-latent vanilla and Matryoshka SAEs (L0=30):
The Matryoshka SAE contains a close-matching latent with .98 correlation with the abstract female tokens latent. In contrast, the closest vanilla latent only fires on variants of 'she'.
Matryoshka often has latents that better match small reference SAE latents. You can check this for yourself by exploring https://sparselatents.com/tree_view.
While I can spot some examples of what look like Matryoshka feature absorption, they seem to be rarer than in vanilla.
To quantify how well large SAEs (inspired by MMCS), I match each reference SAE latent to its highest-correlation counterpart in the large SAE. The mean of these maximum correlations shows how well a large SAE captures the reference SAE's features. For example, for the layer 3 residual stream we have:
Across most model locations (attention out, mlp out, residuals) and for smaller reference SAE sizes, Matryoshka SAEs have higher Mean Max Correlation than vanilla SAEs at the same L0. The exceptions are the residual stream before the first transformer block and the output of the first attention layer. All mean-max correlation graphs can be found in the Appendix.
Reconstruction Quality
Plots of variance explained against L0 (number of active latents) are a common proxy measure for the quality of sparse autoencoders. Unfortunately, feature absorption itself is an effective strategy for reducing the L0 at a fixed FVU. For each parent-child feature relation, a vanilla SAE with feature absorption can represent both features with +1 L0, while an SAE without feature absorption would requires +2 L0. Any solution that removes feature absorption will then likely have worse variance explained against L0.
With this in context, at a fixed L0, Matryoshka SAEs have a slightly worse Fraction of Variance Unexplained (FVU) compared to vanilla SAEs– they often perform comparable to a vanilla SAE 0.4x their size (See Appendix for all graphs).
Better metrics for comparing SAE reconstruction performance against interpretability beyond L0 remain an open problem. The Minimum Description Length paper takes a promising step in this direction.
To train SAEs to hit a particular target L0, I use a simple but effective sparsity regularization controller that was shared with me by Glen Taggart.
Limitations and Future Work
-
Limited SAE and Language Model Training Dataset: The SAEs here were only trained for 100M tokens (1/3 the TinyStories dataset). The language model was trained for 3 epochs on the 300M token TinyStories dataset. It would be good to validate these results with more 'real' language models and train SAEs with much more data.
-
Less-Interpretable Lower Activations: , although small-width SAEs also seem to have this problem some amount. Does this go away with more training or is there a deeper problem here?
-
In the toy model, matryoshka latents corresponding to parent features tend to have larger activations when the children features are active. What's going on with that?
-
The Pareto distribution used for sampling features was selected without much optimization. Would another distribution work better? Is there a way to throw out the distribution-selection entirely, choosing one dynamically over the course of training or via some other creative solution?
-
If two Matryoshka latents are next to each other, the probability that a sampled prefix splits them is low. This seems unlikely to be solved with more prefix losses per batch. I suspect this enables feature absorption when a parent without child and child have very similar probability. Is there a fix for this?
-
Should the Matryoshka prefix-losses be weighted in some way before they're summed?
-
Is there an efficient way to calculate all prefix losses in parallel, instead of a randomly-sampled subset?
-
Reconstruction loss at a fixed L0 isn't the right metric— If true features form a DAG, then including a child node and its parent(s) means having higher L0 than just including the child. What's the right metric? Interpretability as Compression by Ayonrinde et al. is a promising work in this direction.
-
Do Meta-SAEs learn the same features as Matryoshka SAEs?
-
RAVEL is a metric for if SAEs learn latents that specify the country of a location but not that location's continent and vice-versa. It is unclear how models represent continent and country information, but it seems like a plausible candidate for feature-absorption as a location's country implies its continent. Bussman et al. use this metric to benchmark meta-SAEs. How do Matryoshka SAEs perform on this metric?
-
In what ways is the feature-absorption toy model confused and wrong? Is it a reasonable desideratum for an SAE trained on this toy model to learn the specified features? Why or why not?
-
Do Matryoshka SAEs work well with newer SAE architectures like JumpRELU and Crosscoder SAEs?
-
Is there a nice way to extend the Matryoshka method to top-k SAEs?
-
It is unclear how much sparsity regularization should be applied to different latents. How should it be chosen? Would the adaptive regularization method in Rippel et al. 2014 work?
Acknowledgements
I'm extremely grateful for feedback, advice, edits, helpful discussions, and support from Joel Becker, Gytis Daujotas, Julian D'Costa, Leo Gao, Collin Gray, Dan Hendrycks, Benjamin Hoffner-Brodsky, Mason Krug, Hunter Lightman, Mark Lippman, Charlie Rogers-Smith, Logan R. Smith, Glen Taggart, and Adly Templeton.
This research was made possible by funding from Lightspeed Grants.
References
Matryoshka Sparse Autoencoders
Search through latents with a token-regex language
View trees here
View individual latents here
See code here (github.com/noanabeshima/matryoshka-saes)
Abstract
Sparse autoencoders (SAEs)[1][2] break down neural network internals into components called latents. Smaller SAE latents seem to correspond to more abstract concepts while larger SAE latents seem to represent finer, more specific concepts.
While increasing SAE size allows for finer-grained representations, it also introduces two key problems: feature absorption introduced in Chanin et al. [3], where latents develop unintuitive "holes" as other latents in the SAE take over specific cases, and what I term fragmentation, where meaningful abstract concepts in the small SAE (e.g. 'female names' or 'words in quotes') shatter (via feature splitting[1:1]) into many specific latents, hiding real structure in the model.
This paper introduces Matryoshka SAEs, a training approach that addresses these challenges. Inspired by prior work[4][5], Matryoshka SAEs are trained with a sum of SAE losses computed on random prefixes of the SAE latents. I demonstrate that Matryoshka SAEs completely avoid issues in a toy model designed to exhibit feature absorption in traditional SAEs. I then apply the method to a 4-layer TinyStories language model. My results demonstrate that Matryoshka SAEs reduce feature absorption while preserving abstract features.
Introduction
Sparse autoencoders (SAEs) help us break down neural network internals into more easily analyzeable pieces called latents.[1:2][2:1] These latents may correspond to actual "features" the model uses for processing [6][7].
SAE size affects the granularity of learned concepts: smaller SAEs learn abstract latents, while larger ones capture fine details[1:3].
While some splitting of concepts is expected as we increase SAE size, my investigation reveals a consistent pattern of failure:
These issues complicate interpretability work. Feature absorption forces accurate latent descriptions to have lists of special-cased exceptions. Feature fragmentation hides higher-level concepts I think the model likely uses.
Large SAEs offer clear benefits over small ones: better reconstruction error and representation of fine-grained features. Ideally, we'd have a single large SAE that maintain these benefits while preserving the abstract concepts found in smaller SAEs, all without unnatural holes.
While we could use a family of varying size SAEs per language model location, a single SAE per location would be much better for finding feature circuits using e.g. Marks et al's circuit finding method[8].
To address these limitations, I introduce Matryoshka SAEs, an alternative training approach inspired by prior work[4:1][5:1]. In a toy model designed to exhibit feature absorption (similar to the model introduced in Chanin et al.[9]), Matryoshka SAEs completely avoid the feature-absorption holes that appear in vanilla SAEs.
When trained on language models (the output of MLPs, attention blocks, and the residual stream), Large Matryoshka SAEs seem to preserve the abstract features found in small vanilla SAEs better than large vanilla SAEs and appear to have fewer feature-absorption holes.
Problem
Terminology
In this paper, I use 'vanilla' in a somewhat nonstandard way, as I use a log sparsity loss function for both vanilla and Matryoshka SAEs rather than the traditional L1 sparsity loss. This makes them more comparable to sqrt[10] or tanh[7:1][11] sparsity functions. Details can be found here.
Reference SAEs
To study how SAE latents change with scale, I train a family of small vanilla "reference" SAEs of varying sizes (30, 100, 300, 1000, 3k, 10k) on three locations in a 4-layer TinyStories[12] model (https://github.com/noanabeshima/tinymodel): attention block outputs, mlp block outputs, and the residual stream before each attention block. I refer to the 30-latent SAE as S/0, the 100-latent SAE as S/1, etc. where S/x denotes the x-th size in this sequence.
These reference SAEs can help demonstrate both feature absorption and how Matryoshka SAEs preserve abstract latents.
Throughout this paper, any reference SAE without a specified location is trained on the pre-attention residual stream of layer 3 (the model's final layer).
Feature Absorption Example
Let's examine a concrete case of feature absorption by looking at a female-words latent in the 300-latent reference SAE (S/2) and some handpicked latents it co-fires with in the 1000-latent SAE (S/3). S/2/65 (latent 65 of S/2) and S/3/66 look very similar to each other. If you're curious, you might try to spot their differences using this interface:
The root node, S/2/65, seems to fire on female names, ' she', ' her', and ' girl'. Some rarer tokens I notice while sampling include daughter, lady, aunt, queen, pink, and doll.
If you click on the right node, S/3/861, you'll see that it seems to be a Sue feature. S/3/359 is similar to the Sue latent but for Lily, Lilly, Lila, and Luna.
S/3/66, however, is very interesting. It's very similar to its parent, S/2/101, except for specific *holes—*it often skips Lily or Sue tokens! You can see this by clicking on S/2/65 and then hovering on-and-off S/3/66.
The abstract female concept is likely still implicitly represented in the SAE for Lily and Sue—it's included in the Lily and Sue latent decoder vectors. But we can't detect that just by looking at activations anymore. The concept has become invisible. In exchange, our larger SAE now represents the new information that Lily and Sue are distinct names.
Larger width SAEs with the same L0 stop representing a feature that fires on most female names. The feature has become fragmented across many latents for particular names. If every name has its own latent, you can't tell that the language model knows that some names are commonly female from the SAE activations alone.
Feature fragmentation also complicates circuit analysis using SAEs (see Marks et al.[12:1]). If a circuit uses a concept like 'this token is a name', we don't want to trace through 100 different name-specific latents when a single 'name' latent would suffice. On the other hand, if a circuit uses fine-grained features, we want our SAE to capture those too. When looking for a circuit, it is not obvious how to choose the appropriate vanilla SAE size for many different locations in the model simultaneously. And if the circuit depends on both an abstract and fine-grained feature in one location, no single vanilla SAE size is sufficient and it is unclear how to effectively integrate multiple sizes.
More examples of absorption and fragmentation can be found in https://sparselatents.com/tree_view.
Method
Consider how feature absorption might occur during SAE training:
How can we stop the SAE from absorbing features like this?
What if we could stop absorption by sometimes training our abstract latents without the specific latents present? Then a "female tokens" latent would need to learn to fire on all female tokens, including "Lily", since there wouldn't be a consistent "Lily" latent to rely on.
This is the idea for the Matryoshka SAE: train on a mixture of losses, each computed on a different prefix of the SAE latents.
The Matryoshka SAE computes multiple SAE losses in each training step, each using a different-length prefix of the autoencoder latents. When computing losses with shorter prefixes, early latents must reconstruct the input without help from later latents. This reduces feature absorption - an early "female words" latent can't rely on a later "Lily-specific" latent to handle Lily tokens, since that later latent isn't always available. Later latents are then free to specialize without creating holes in earlier, more abstract features.
For each batch, I compute losses using 10 different prefixes. One prefix is the entire SAE, and the remaining prefix lengths are sampled from a truncated Pareto distribution. Always including the entire SAE prefix avoids the issue where SAE latents later in the ordering aren't trained on many examples because their probability of being sampled in at least one prefix is low.
At every batch, I reorder the SAE latents based on their contribution to reconstruction—latents with larger squared activations (weighted by decoder norm) are moved earlier. This ensures that important features consistently appear in shorter prefixes.
A naive implementation would require 10 forward passes per batch, and could be quite slow. By reusing work between prefixes, my algorithm trains in only 1.5x the time of a standard SAE. Mathematical details and efficient training algorithm can be found in https://www.sparselatents.com/matryoshka_loss.pdf. Code can be found at github.com/noanabeshima/matryoshka-saes.
Results
Toy Model
To demonstrate how Matryoshka SAEs prevent feature absorption, I first test them on a toy model, similar to the model introduced in Chanin et al. [8:1], where we can directly observe feature absorption happening for vanilla SAEs.
Features in this toy model form a tree, where child features only appear if their parent features are present. Just as "Lily" always implies "female name" in our language model example, child features here are always accompanied by their parent features.
Each edge in the tree has an assigned probability, determining whether a child feature appears when its parent is present. The root node is always sampled but isn't counted as a feature. Each feature corresponds to a random orthogonal direction in a 30-dimensional space, with magnitude roughly 1 (specifically, 1 + normal(0, 0.05)). Features are binary—they're either present or absent with no noise. I set the number of SAE latents to the number of features.
Let's look at how vanilla and Matryoshka SAEs learn these features after training for 20K steps with Adam. Below are the ground-truth features on a batch of data with all-zero entries filtered out.
The vanilla SAE activations show feature-absorption holes—parent features don't fire when their children fire:
The Matryoshka SAE latents, however, match the ground truth pattern—each latent fires whenever its corresponding feature is present.
Interestingly, matryoshka parents tend to have slightly larger activations when their children are present.
Here are the cosine similarities between the ground truth features and the vanilla and Matryoshka SAE decoders.
Language Model Results
To test Matryoshka SAEs on real neural networks, I train 25k-latent vanilla and Matryoshka SAEs with varying L0s [15, 30, 60] on different locations (the output of MLPs, attention blocks, and the residual stream) in a TinyStories language model. They're trained on 100M tokens, 1/3 the size of the TinyStories dataset.
Let's return to our female words example. Below, each reference SAE latent is shown alongside its closest match (by activation correlation) from both the 25k-latent vanilla and Matryoshka SAEs (L0=30):
The Matryoshka SAE contains a close-matching latent with .98 correlation with the abstract female tokens latent. In contrast, the closest vanilla latent only fires on variants of 'she'.
Matryoshka often has latents that better match small reference SAE latents. You can check this for yourself by exploring https://sparselatents.com/tree_view.
While I can spot some examples of what look like Matryoshka feature absorption, they seem to be rarer than in vanilla.
To quantify how well large SAEs preserve reference SAE features (inspired by MMCS[13]), I match each reference SAE latent to its highest-correlation counterpart in the large SAE. The mean of these maximum correlations shows how well a large SAE captures the reference SAE's features. For example, for the layer 3 residual stream we have:
Across most model locations (attention out, mlp out, residuals) and for smaller reference SAE sizes, Matryoshka SAEs have higher Mean Max Correlation than vanilla SAEs at the same L0. The exceptions are the residual stream before the first transformer block and the output of the first attention layer. All mean-max correlation graphs can be found in the Appendix.
Reconstruction Quality
Plots of variance explained against L0 (number of active latents) are a common proxy measure for the quality of sparse autoencoders. Unfortunately, feature absorption itself is an effective strategy for reducing the L0 at a fixed FVU. For each parent-child feature relation, a vanilla SAE with feature absorption can represent both features with +1 L0, while an SAE without feature absorption would requires +2 L0. Any solution that removes feature absorption will then likely have worse variance explained against L0.
With this in context, at a fixed L0, Matryoshka SAEs have a slightly worse Fraction of Variance Unexplained (FVU) compared to vanilla SAEs– they often perform comparable to a vanilla SAE 0.4x their size (See Appendix for all graphs).
Better metrics for comparing SAE reconstruction performance against interpretability beyond L0 remain an open problem. The Minimum Description Length paper [14] takes a promising step in this direction.
To train SAEs to hit a particular target L0, I use a simple but effective sparsity regularization controller that was shared with me by Glen Taggart.[15]
Limitations and Future Work
Limited SAE and Language Model Training Dataset: The SAEs here were only trained for 100M tokens (1/3 the TinyStories[11:1] dataset). The language model was trained for 3 epochs on the 300M token TinyStories dataset. It would be good to validate these results with more 'real' language models and train SAEs with much more data.
Less-Interpretable Lower Activations: Matryoshka sometimes seem to have less-interpretable lower activations than vanilla, although small-width SAEs also seem to have this problem some amount. Does this go away with more training or is there a deeper problem here?
In the toy model, matryoshka latents corresponding to parent features tend to have larger activations when the children features are active. What's going on with that?
The Pareto distribution used for sampling features was selected without much optimization. Would another distribution work better? Is there a way to throw out the distribution-selection entirely, choosing one dynamically over the course of training or via some other creative solution?
If two Matryoshka latents are next to each other, the probability that a sampled prefix splits them is low. This seems unlikely to be solved with more prefix losses per batch. I suspect this enables feature absorption when a parent without child and child have very similar probability. Is there a fix for this?
Should the Matryoshka prefix-losses be weighted in some way before they're summed?
Is there an efficient way to calculate all prefix losses in parallel, instead of a randomly-sampled subset?
Reconstruction loss at a fixed L0 isn't the right metric— If true features form a DAG, then including a child node and its parent(s) means having higher L0 than just including the child. What's the right metric? Interpretability as Compression by Ayonrinde et al.[14:1] is a promising work in this direction.
Do Meta-SAEs[16] learn the same features as Matryoshka SAEs?
RAVEL[17] is a metric for if SAEs learn latents that specify the country of a location but not that location's continent and vice-versa. It is unclear how models represent continent and country information, but it seems like a plausible candidate for feature-absorption as a location's country implies its continent. Bussman et al. use this metric to benchmark meta-SAEs[16:1]. How do Matryoshka SAEs perform on this metric?
In what ways is the feature-absorption toy model confused and wrong? Is it a reasonable desideratum for an SAE trained on this toy model to learn the specified features? Why or why not?
Do Matryoshka SAEs work well with newer SAE architectures like JumpRELU and Crosscoder SAEs?
Is there a nice way to extend the Matryoshka method to top-k SAEs?
It is unclear how much sparsity regularization should be applied to different latents. How should it be chosen? Would the adaptive regularization method in Rippel et al. 2014[5:2] work?
Acknowledgements
I'm extremely grateful for feedback, advice, edits, helpful discussions, and support from Joel Becker, Gytis Daujotas, Julian D'Costa, Leo Gao, Collin Gray, Dan Hendrycks, Benjamin Hoffner-Brodsky, Mason Krug, Hunter Lightman, Mark Lippman, Charlie Rogers-Smith, Logan R. Smith, Glen Taggart, and Adly Templeton.
This research was made possible by funding from Lightspeed Grants.
References
Towards Monosemanticity: Decomposing Language Models With Dictionary Learning [link]
Bricken, T., Templeton, A., Batson, J., Chen, B., Jermyn, A., Conerly, T., Turner, N., Anil, C., Denison, C., Askell, A., Lasenby, R., Wu, Y., Kravec, S., Schiefer, N., Maxwell, T., Joseph, N., Hatfield-Dodds, Z., Tamkin, A., Nguyen, K., McLean, B., Burke, J.E., Hume, T., Carter, S., Henighan, T. and Olah, C., 2023. Transformer Circuits Thread. ↩︎ ↩︎ ↩︎ ↩︎
Sparse Autoencoders Find Highly Interpretable Features in Language Models [link]
Cunningham, H., Ewart, A., Riggs, L., Huben, R. and Sharkey, L., 2023. arXiv preprint arXiv:2309.08600. ↩︎ ↩︎
A is for Absorption: Studying Feature Splitting and Absorption in Sparse Autoencoders [link]
Chanin, D., Wilken-Smith, J., Dulka, T., Bhatnagar, H. and Bloom, J., 2024. arXiv preprint arXiv:2409.14507. ↩︎ ↩︎
Matryoshka Representation Learning [link]
Kusupati, A., Bhatt, G., Rege, A., Wallingford, M., Sinha, A., Ramanujan, V., Howard-Snyder, W., Chen, K., Kakade, S., Jain, P. and Farhadi, A., 2022. arXiv preprint arXiv:2205.13147. ↩︎ ↩︎
Learning Ordered Representations with Nested Dropout [link]
Rippel, O., Gelbart, M.A. and Adams, R.P., 2014. arXiv preprint arXiv:1402.0915. Published in ICML 2014. ↩︎ ↩︎ ↩︎
Zoom In: An Introduction to Circuits [link]
Olah, C., Cammarata, N., Schubert, L., Goh, G., Petrov, M. and Carter, S., 2020. Distill. DOI: 10.23915/distill.00024.001 ↩︎
Tanh Penalty in Dictionary Learning [link]
Jermyn, A. et al., 2024. Transformer Circuits. ↩︎ ↩︎
Toy Models of Feature Absorption in SAEs [link]
Chanin, D., Bhatnagar, H., Dulka, T. and Bloom, J., 2024. LessWrong. ↩︎ ↩︎
Improving SAE's by Sqrt()-ing L1 & Removing Lowest Activating Features [link]
Riggs, L. and Brinkmann, J., 2024. AI Alignment Forum. ↩︎
Interpretability Evals for Dictionary Learning [link]
Lindsey, J., Cunningham, H. and Conerly, T., 2024. Ed. by A. Templeton. Transformer Circuits. ↩︎
TinyStories: How Small Can Language Models Be and Still Speak Coherent English? [link]
Eldan, R. and Li, Y., 2023. arXiv preprint arXiv:2305.07759. ↩︎ ↩︎
Sparse Feature Circuits: Discovering and Editing Interpretable Causal Graphs in Language Models [link]
Marks, S., Rager, C., Michaud, E.J., Belinkov, Y., Bau, D. and Mueller, A., 2024. arXiv preprint arXiv:2403.19647. ↩︎ ↩︎
[Interim research report] Taking features out of superposition with sparse autoencoders [link]
Sharkey, L., Braun, D. and Millidge, B., 2022. AI Alignment Forum. ↩︎
Interpretability as Compression: Reconsidering SAE Explanations of Neural Activations with MDL-SAEs [link]
Ayonrinde, K., Pearce, M.T. and Sharkey, L., 2024. arXiv preprint arXiv:2410.11179. ↩︎ ↩︎
To-be-published L0 targeting paper
Taggart, G. 2024/2025. ↩︎
Showing SAE Latents Are Not Atomic Using Meta-SAEs [link]
Bussmann, B., Pearce, M., Leask, P., Bloom, J., Sharkey, L. and Nanda, N., 2024. AI Alignment Forum. ↩︎ ↩︎
Evaluating Open-Source Sparse Autoencoders on Disentangling Factual Knowledge in GPT-2 Small [link]
Chaudhary, M. and Geiger, A., 2024. arXiv preprint arXiv:2409.04478. ↩︎